Обработка данных
Когда Вы имеете дело с выборкой экспериментальных данных, то они, чаще всего, представляются в виде массива, состоящего из пар чисел (xi, yi). Поэтому возникает задача аппроксимации дискретной зависимости y(xj непрерывной функцией f(x). Функция f(x), в зависимости от специфики задачи, может отвечать различным требованиям:
- f(x) должна проходить через точки (xi, yi), т.е. f (хi)=уi, i=1...n. В этом случае (см. разд. 15.1) говорят об интерполяции данных функцией f (х) во внутренних точках между хi, или экстраполяции за пределами интервала, содержащего все хi;
- f (х) должна некоторым образом (например в виде определенной аналитической зависимости) приближать y(xi), не обязательно проходя через точки (xi, yi). Такова постановка задачи регрессии (см. разд. 15.2), которую во многих случаях также можно назвать сглаживанием данных;
- f (х) должна приближать экспериментальную зависимость y(xi), учитывая к тому же, что данные (xi, yi) получены с некоторой погрешностью, выражающей шумовую компоненту измерений. При этом функция f (х), с помощью того или иного алгоритма, уменьшает погрешность, присутствующую в данных (xi, yi). Такого типа задачи называют задачами фильтрации (см. разд. 15.3). Сглаживание — частный случай фильтрации.
Различные виды построения аппроксимирующей зависимости f (х) иллюстрирует рис. 15.1. На нем исходные данные обозначены кружками, интерполяция отрезками прямых линий — пунктиром, линейная регрессия — наклонной прямой линией, а фильтрация — жирной гладкой кривой. Эти зависимости приведены в качестве примера и отражают лишь малую часть возможностей Mathcad по обработке данных. Вообще говоря, в Mathcad имеется целый арсенал встроенных функций, позволяющий осуществлять самую различную регрессию, интерполяцию-экстраполяцию и сглаживание данных.
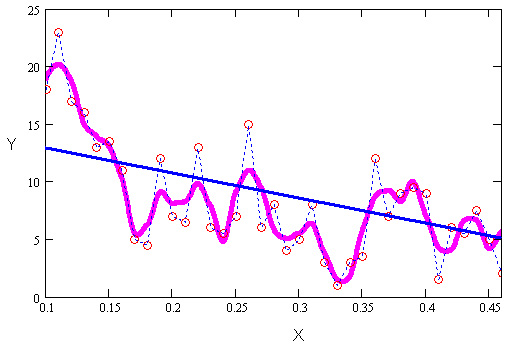
Рис. 15.1. Разные задачи аппроксимации данных
Как в целях подавления шума, так и для решения других проблем обработки данных, широко применяются различные интегральные преобразования. Они ставят в соответствие всей совокупности данных у(х) некоторую функцию другой координаты (или координат) F(CO). Примерами интегральных преобразований являются преобразование Фурье (см. разд. 15.4.1) и вейвлетное преобразование (см. разд. 15.4.2). Напомним, что некоторые преобразования, например Фурье и Лапласа, можно осуществить в режиме символьных вычислений (см. гл. 5). Каждое из интегральных преобразований эффективно для решения своего круга задач анализа данных.
Для построения интерполяции-экстраполяции в Mathcad имеются несколько встроенных функций, позволяющих "соединить" точки выборки данных (xi, yi) кривой разной степени гладкости. По определению интерполяция означает построение функции д(х), аппроксимирующей зависимость у(х) в промежуточных точках (между xi). Поэтому интерполяцию еще по-другому называют аппроксимацией. В точках xi значения интерполяционной функции должны совпадать с исходными данными, т. е. A(xi) =у(xi).
Везде в этом разделе при рассказе о различных типах интерполяции будем использовать вместо обозначения А(Х) другое имя ее аргумента A(t), чтобы не путать вектор данных х и скалярную переменную t.
Самый простой вид интерполяции — линейная, которая представляет искомую зависимость А(Х) в виде ломаной линии. Интерполирующая функция А(Х) состоит из отрезков прямых, соединяющих точки (рис. 15.2).
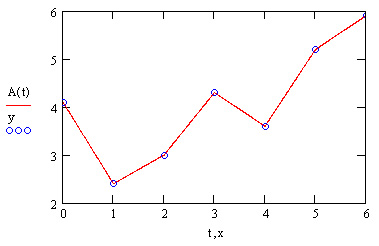
Рис. 15.2. Линейная интерполяция (листинг 15.1)
Для построения линейной интерполяции служит встроенная функция linterp (листинг 15.1).
- linterp(x, y, t) — функция, аппроксимирующая данные векторов х и у кусочно-линейной зависимостью;
- х — вектор действительных данных аргумента;
- у — вектор действительных данных значений того же размера;
- t — значение аргумента, при котором вычисляется интерполирующая функция.
Элементы вектора х должны быть определены в порядке возрастания, т. е. Х1<Х2<Х3< . . . <Xn.
Листинг 15.1. Линейная интерполяция

Как видно из листинга, чтобы осуществить линейную интерполяцию, надо выполнить следующие действия:
- Введите векторы данных х и у (первые две строки листинга).
- Определите функцию linterp(х,у, t).
- Вычислите значения этой функции в требуемых точках, например lin-terp(x,y, 2.4)=3.52 или iinterp(x,y,6) =5.9, или постройте ее график, как показано на рис. 15.2.
Обратите внимание, что функция A(t) на графике имеет аргумент t, а не х. Это означает, что функция А (с) вычисляется не только при значениях аргумента (т. е. в семи точках), а при гораздо большем числе аргументов в интервале (0,6), что автоматически обеспечивает Mathcad. Просто в данном случае эти различия незаметны, т. к. при обычном построении графика функции А(х) от векторного аргумента х (рис. 15.3) Mathcad, по умолчанию, соединяет точки графика прямыми линиями (т. е. скрытым образом осуществляет их линейную интерполяцию).
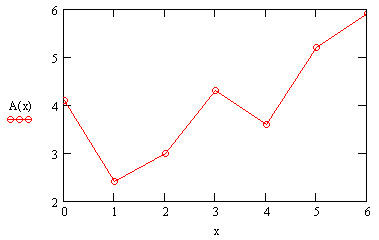
Рис. 15.3. Обычное построение графика функции от векторной переменной х (листинг 15.1)
15.1.2. Кубическая сплайн-интерполяция
В большинстве практических приложений желательно соединить экспериментальные точки не ломаной линией, а гладкой кривой. Лучше всего для этих целей подходит интерполяция кубическими сплайнами, т. е. отрезками кубических парабол (рис. 15.4).
- interp(s,x,y,t) — функция, аппроксимирующая данные векторов х и у кубическими сплайнами;
- s — вектор вторых производных, созданный одной из сопутствующих функций cspline, pspline или lspline;
- х — вектор действительных данных аргумента, элементы которого расположены в порядке возрастания;
- у — вектор действительных данных значений того же размера;
- t — значение аргумента, при котором вычисляется интерполирующая функция.
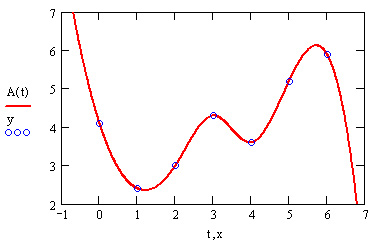
Рис. 15.4. Сплайн-интерполяция (см. листинг 15.2)
Сплайн-интерполяция в Mathcad реализована чуть сложнее линейной. Перед применением функции interp необходимо предварительно определить первый из ее аргументов — векторную переменную s. Делается это при помощи одной из трех встроенных функций тех же аргументов (х,у).
- lspline(x,y) — вектор значений коэффициентов линейного сплайна;
- pspline(x,y) — вектор значений коэффициентов квадратичного сплайна;
- cspline(x,y) — вектор значений коэффициентов кубического сплайна;
- х, у — векторы данных.
Выбор конкретной функции сплайновых коэффициентов влияет на интерполяцию вблизи конечных точек интервала. Пример сплайн-интерполяции приведен в листинге 15.2.
Листинг 15.2. Кубическая сплайн-интерполяция

Смысл сплайн-интерполяции заключается в том, что в промежутках между точками осуществляется аппроксимация в виде зависимости A(t) = =а t3+bt2+ct+d. Коэффициенты а, b, с, d рассчитываются независимо для каждого промежутка, исходя из значений уг в соседних точках. Этот процесс скрыт от пользователя, поскольку смысл задачи интерполяции состоит в выдаче значения A(t) в любой точке t (рис. 15.4).
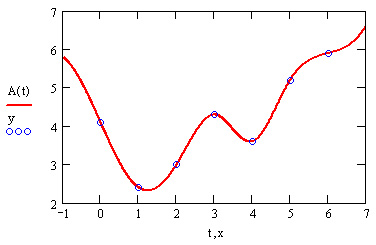
Рис. 15.5. Сплайн-интерполяция с выбором коэффициентов линейного сплайна lspline
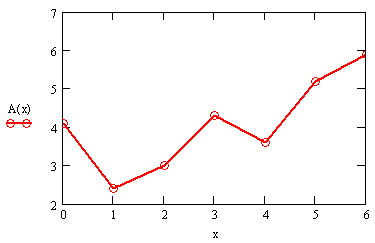
Рис. 15.6. Ошибочное построение графика сплайн-интерполяции (см. листинг 15.2)
Чтобы подчеркнуть различия, соответствующие разным вспомогательным функциям cspline, pspline, Ispline, покажем результат действия листинга 15.2 при замене функции cspline в предпоследней строке на линейную ispiine (рис. 15.5). Как видно, выбор вспомогательных функций существенно влияет на поведение A(t) вблизи граничных точек рассматриваемого интервала (0, 6) и особенно разительно меняет результат экстраполяции данных за его пределами.
В заключение остановимся на уже упоминавшейся в предыдущем разделе распространенной ошибке при построении графиков интерполирующей функции (см. рис. 15.3). Если на графике, например являющемся продолжением листинга 15.2, задать построение функции А(Х) вместо A(t), то будет получено просто соединение исходных точек ломаной (рис. 15.6). Так происходит потому, что в промежутках между точками вычисления интерполирующей функции не производятся.
15.1.3. Полиномиальная сплайн-интерполяция
Более сложный тип интерполяции — так называемая интерполяция В-сплай-нами. В отличие от обычной сплайн-интерполяции (см. разд. 15.1.2), сшивка элементарных В-сплайнов производится не в точках хi а в других точках ui, координаты которых предлагается ввести пользователю. Сплайны могут быть полиномами 1, 2 или 3 степени (линейные, квадратичные или кубические). Применяется интерполяция В-сплайнами точно так же, как и обычная сплайн-интерполяция, различие состоит только в определении вспомогательной функции коэффициентов сплайна.
- interp(s,x,y, t) — функция, аппроксимирующая данные векторов х и у с помощью В-сплайнов;
- bspline(x,y,u,n) — вектор значений коэффициентов В-сплайна;
- s — вектор вторых производных, созданный функцией bspline;
- х — вектор действительных данных аргумента, элементы которого расположены в порядке возрастания;
- у — вектор действительных данных значений того же размера;
- t — значение аргумента, при котором вычисляется интерполирующая функция;
- u — вектор значений аргумента, в которых производится сшивка В-сплайнов;
- n — порядок полиномов сплайновой интерполяции (1, 2 или 3).
Размерность вектора и должна быть на 1, 2 или з меньше размерности векторов х и у. Первый элемент вектора и должен быть меньше или равен первому элементу вектора х, а последний элемент и — больше или равен последнему элементу х.
Интерполяция В-сплайнами иллюстрируется листингом 15.3 и рис. 15.7.
Листинг 15.3. Интерполяция В-сплайнами

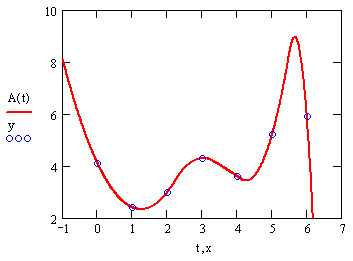
Рис. 15.7. В-сплайн-интерполяция (листинг 15.3)
15.1.4. Экстраполяция функцией предсказания
Все рассмотренные выше (см. разд. 15.1.1—15.1.3) функции осуществляли экстраполяцию данных за пределами их интервала с помощью соответствующей зависимости, основанной на анализе расположения нескольких исходных точек на границах интервала. В Mathcad имеется более развитый инструмент экстраполяции, который учитывает распределение данных вдоль всего интервала. В функцию predict встроен линейный алгоритм предсказания поведения функции, основанный на анализе, в том числе осцилляции.
- predict (у,m,n) — функция предсказания вектора, экстраполирующего выборку данных;
- у — вектор действительных значений, взятых через равные промежутки значений аргумента;
- m — количество последовательных элементов вектора у, согласно которым строится экстраполяция;
- n— количество элементов вектора предсказаний.
Пример использования функции предсказания на примере экстраполяции осциллирующих данных yi с меняющейся амплитудой приведен в листинге 15.4. Полученный график экстраполяции, наряду с самой функцией, показан на рис. 15.8. Аргументы и принцип действия функции predict отличаются от рассмотренных выше встроенных функций интерполяции-экстраполяции. Значений аргумента для данных не требуется, поскольку по определению функция действует на данные, идущие друг за другом с равномерным шагом. Обратите внимание, что результат функции predict вставляется "в хвост" исходных данных.
Листинг 15.4. Экстраполяция при помощи функции предсказания
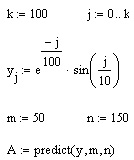
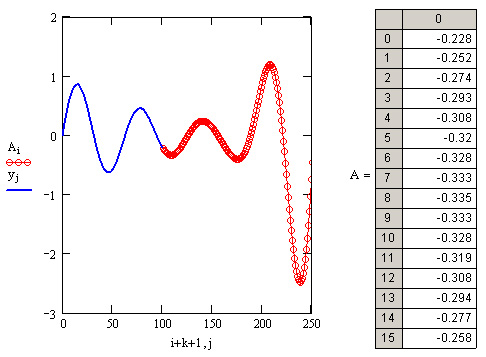
Рис. 15.8. Экстраполяция при помощи функции предсказания (листинг 15.4)
Как видно из рис. 15.9, функция предсказания может быть полезна при экстраполяции данных на небольшие расстояния. Вдали от исходных данных результат часто бывает неудовлетворительным. Кроме того, функция predict хорошо работает в задачах анализа подробных данных с четко прослеживающейся закономерностью (типа рис. 15.8), в основном осциллирующего характера.
Если данных мало, то предсказание может оказаться бесполезным. В листинге 15.5 приведена экстраполяция небольшой выборки данных (из примеров, рассмотренных в предыдущих разделах). Соответствующий результат показан на рис. 15.9 для различных крайних точек массива исходных данных, для которых строится экстраполяция.
Листинг 15.5. Экстраполяция при помощи функции предсказания

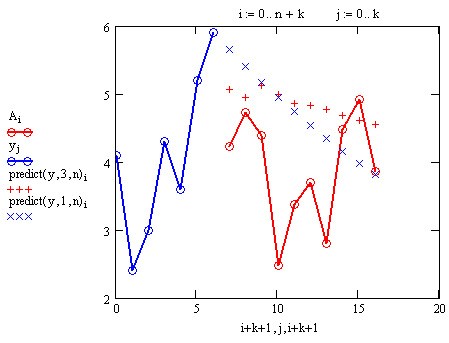
Рис. 15.9. Работа функции предсказания в случае малого количества данных (листинг 15.5)
15.1.5. Многомерная интерполяция
Двумерная сплайн-интерполяция приводит к построению поверхности z(x,y), проходящей через массив точек, описывающий сетку на координатной плоскости (х,у). Поверхность создается участками двумерных кубических сплайнов, являющихся функциями (х,у) и имеющих непрерывные первые и вторые производные по обеим координатам.
Многомерная интерполяция строится с помощью тех же встроенных функций, что и одномерная (см. разд. 15.1.2), но имеет в качестве аргументов не векторы, а соответствующие матрицы. Существует одно важное ограничение, связанное с возможностью интерполяции только квадратных NXN массивов данных.
- interp(s,x,z,v) — скалярная функция, аппроксимирующая данные выборки двумерного поля по координатам х и у кубическими сплайнами;
- s — вектор вторых производных, созданный одной из сопутствующих функций cspline, pspline или lspline;
- х — матрица размерности Nx2, определяющая диагональ сетки значений аргумента (элементы обоих столбцов соответствуют меткам х и у и расположены в порядке возрастания);
- z — матрица действительных данных размерности NXN;
- v — вектор из двух элементов, содержащий значения аргументов х и у, для которых вычисляется интерполяция.
Вспомогательные функции построения вторых производных имеют те же матричные аргументы, что и interp: Ispline (X,Y), pspline (X, У), cspline(X,Y).
Пример исходных данных приведен на рис. 15.10 в виде графика линий уровня, программная реализация двумерной интерполяции показана в листинге 15.6, а ее результат — на рис. 15.11.
Листинг 15.6. Двумерная интерполяция

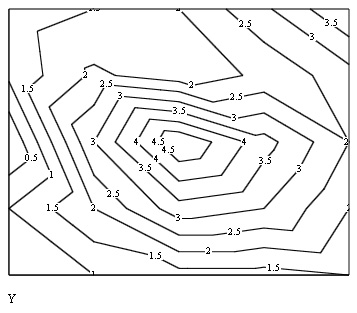
Рис. 15.10.Исходное двумерное поле данных (листинг 15.6)
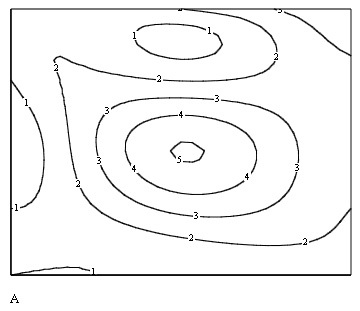
Рис. 15.11. Результат двумерной интерполяции (листинг 15.6)
Задачи математической регрессии имеют смысл приближения выборки данных (Xi..Yi некоторой функцией f (х), определенным образом минимизирующей совокупность ошибок |f(xi)-yi|. Регрессия сводится к подбору неизвестных коэффициентов, определяющих аналитическую зависимость f(х). В силу производимого действия большинство задач регрессии являются частным случаем более общей проблемы сглаживания данных.
Как правило, регрессия очень эффективна, когда заранее известен (или, по крайней мере, хорошо угадывается) закон распределения данных (xi, yi).
Самый простой и наиболее часто используемый вид регрессии — линейная. Приближение данных (xi, yi) осуществляется линейной функцией у(х)=b+ах. На координатной плоскости (х,у) линейная функция, как известно, представляется прямой линией (рис. 15.12). Еще линейную регрессию часто называют методом наименьших квадратов, поскольку коэффициенты а и ь вычисляются из условия минимизации суммы квадратов ошибок |b+axi-yi|.
Чаще всего такое же условие ставится и в других задачах регрессии, т. е. приближения массива данных (хi,уi) другими зависимостями у(х). Исключение рассмотрено в листинге 15.9.
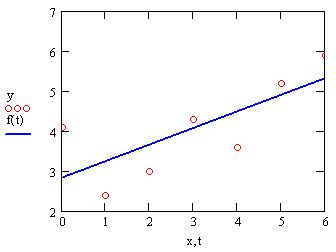
Рис. 15.12. Линейная регрессия (листинг 15.7 или 15.8)
Для расчета линейной регрессии в Mathcad имеются два дублирующих друг друга способа. Правила их применения представлены в листингах 15.7 и 15.8. Результат обоих листингов получается одинаковым (рис. 15.12).
- line(x,y) — вектор из двух элементов (b,а) коэффициентов линейной регрессии ь+а-х;
- intercept (x,y) — коэффициент b линейной рефессии;
- slope(x,y) — коэффициент а линейной рефессии;
- х — вектор действительных данных аргумента;
- у — вектор действительных данных значений того же размера.
Листинг 15.7. Линейная регрессия
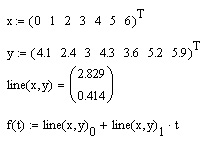
Листинг 15.8. Другая форма записи линейной регрессии

В Mathcad имеется альтернативный алгоритм, реализующий не минимизацию суммы квадратов ошибок, а медиан-медианную линейную рефессию для расчета коэффициентов а и ь (листинг 15.9).
- medfit(x,y) — вектор из двух элементов (b,а) коэффициентов линейной медиан-медианной рефессии b+ах;
- х,у — векторы действительных данных одинакового размера.
Листинг 15.9. Построение линейной регрессии двумя разными иетодами (продолжение листинга 15.7)
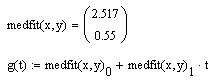
Различие результатов среднеквадратичной и медиан-медианной рефессии иллюстрируется рис. 15.13.
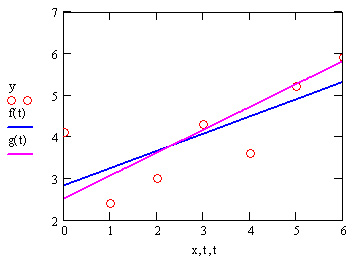
Рис. 15.13. Линейная регрессия по методу наименьших квадратов и методу медиан (листинги 15.7 и 15.9)
15.2.2. Полиномиальная регрессия
В Mathcad реализована регрессия одним полиномом, отрезками нескольких полиномов, а также двумерная регрессия массива данных.
Полиномиальная регрессия
Полиномиальная регрессия означает приближение данных (xi, yi) полиномом k-й степени А(х)=а+bх+сх2+dх3+.. .+hxk (рис. 15.14). При k=1 полином является прямой линией, при k=2 — параболой, при k=3 — кубической параболой и т. д. Как правило, на практике применяются k<5.
Для построения регрессии полиномом k-й степени необходимо наличие по крайней мере (k+1) точек данных.
В Mathcad полиномиальная регрессия осуществляется комбинацией встроенной функции regress и полиномиальной интерполяции (см. разд. 15.1.2).
- regress(x,y,k) — вектор коэффициентов для построения полиномиальной регрессии данных;
- interp(s,x,y, t) — результат полиномиальной регрессии;
- s=regress(x,y,k);
- х — вектор действительных данных аргумента, элементы которого расположены в порядке возрастания;
- у — вектор действительных данных значений того же размера;
- k — степень полинома регрессии (целое положительное число);
- t — значение аргумента полинома регрессии.
Для построения полиномиальной регрессии после функции regress Вы обязаны использовать функцию interp.
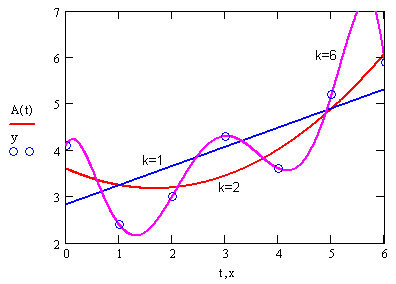
Рис. 15.14. Регрессия полиномами разной степени (коллаж результатов листинга 15.10 для разных k)
Пример полиномиальной регрессии квадратичной параболой приведен в листинге 15.10.
Листинг 15.10. Полиноминальная регрессия

Регрессия отрезками полиномов
Помимо приближения массива данных одним полиномом имеется возможность осуществить регрессию сшивкой отрезков (точнее говоря, участков, т. к. они имеют криволинейную форму) нескольких полиномов. Для этого имеется встроенная функция loess, применение которой аналогично функции regress (листинг 15.11 и рис. 15.15).
- loess (x,у, span) — вектор коэффициентов для построения регрессии данных отрезками полиномов;
- interp(s,x,y,t) — результат полиномиальной регрессии;
- s=loess(x,y,span);
- х — вектор действительных данных аргумента, элементы которого расположены в порядке возрастания;
- у — вектор действительных данных значений того же размера;
- span — параметр, определяющий размер отрезков полиномов (положительное число, хорошие результаты дает значение порядка span=0 .75).
Параметр span задает степень сглаженности данных. При больших значениях span регрессия практически не отличается от регрессии одним полиномом (например, span=2 дает почти тот же результат, что и приближение точек параболой).
Листинг 15.11. Регрессия отрезками полиномов

Регрессия одним полиномом эффективна, когда множество точек выглядит как полином, а регрессия отрезками полиномов оказывается полезной в противоположном случае.
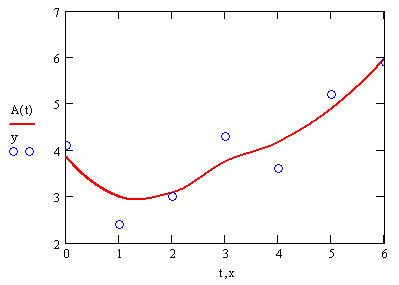
Рис. 15.15. Регрессия отрезками полиномов (листинг 15.11)
Двумерная полиномиальная регрессия
По аналогии с одномерной полиномиальной регрессией и двумерной интерполяцией (см. разд. 15.1.5) Mathcad позволяет приблизить множество точек zi,j(хi, уi) поверхностью, которая определяется многомерной полиномиальной зависимостью. В качестве аргументов встроенных функций для построения полиномиальной регрессии должны стоять в этом случае не векторы, а соответствующие матрицы.
- regress(x,z,k) — вектор коэффициентов для построения полиномиальной регрессии данных;
- loess (x,z, span) — вектор коэффициентов для построения регрессии данных отрезками полиномов;
- interp(s,x,z,v) — скалярная функция, аппроксимирующая данные выборки двумерного поля по координатам х и у кубическими сплайнами;
- s — вектор вторых производных, созданный одной из сопутствующих функций loess или regress;
- х — матрица размерности NX2, определяющая пары значений аргумента (столбцы соответствуют меткам х и у);
- z — вектор действительных данных размерности N;
- span — параметр, определяющий размер отрезков полиномов;
- k — степень полинома регрессии (целое положительное число);
- v — вектор из двух элементов, содержащий значения аргументов х и у, для которых вычисляется интерполяция.
Для построения регрессии не предполагается никакого предварительного упорядочивания данных (как, например, для двумерной интерполяции, которая требует их представления в виде матрицы NXN). В связи с этим данные представляются как вектор.
Двумерная полиномиальная регрессия иллюстрируется листингом 15.12 и рис. 15.16. Сравните стиль представления данных для двумерной регрессии с представлением тех же данных для двумерной сплайн-интерполяции (см. листинг 15.6) и ее результаты с исходными данными (см. рис. 15.10) и их сплайн-интерполяцией (см. рис. 15.11).
Листинг 15.12. Двумерная полиномиальная регрессия

Обратите внимание на знаки транспонирования в листинге. Они применены для корректного представления аргументов (например z в качестве вектора, а не строки).
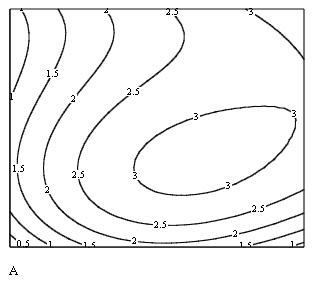
Рис. 15.16. Двумерная полиномиальная регрессия (листинг 15.12)
15.2.3. Регрессия специального вида
Кроме рассмотренных, в Mathcad встроено еще несколько видов трехпара-метрической регрессии. Их реализация несколько отличается от приведенных выше вариантов регрессии тем, что для них, помимо массива данных, требуется задать некоторые начальные значения коэффициентов а,ь,с. Используйте соответствующий вид регрессии, если хорошо представляете себе, какой зависимостью описывается Ваш массив данных. Когда тип регрессии плохо отражает последовательность данных, то ее результат часто бывает неудовлетворительным и даже сильно различающимся в зависимости от выбора начальных значений. Каждая из функций выдает вектор уточненных параметров а,b,с.
- expfit(x,y,g) —регрессия экспонентой f(x)=aebx+c;
- lgsfit(x,y,g) —регрессия логистической функцией f (x)=a/ (1+bесх);
- sinf it (x,y,g) —регрессия синусоидой f(x) =asin (х+b)+с;
- pwfit(x,y,g) — регрессия степенной функцией f(x)=axb+c;
- iogfit(x,y,g) — рефессия логарифмической функцией f(x) =aln(х+b)+с;
- lnfit(x,y) — регрессия двухпараметрической логарифмической функцией f(x)=aln(x)+b;
- х — вектор действительных данных аргумента;
- у — вектор действительных значений того же размера;
- g — вектор из трех элементов, задающий начальные значения а,b,с.
Правильность выбора начальных значений можно оценить по результату регрессии — если функция, выданная Mat head, хорошо приближает зависимость у (х), значит они были подобраны удачно.
Пример расчета одного из видов трехпараметрической регрессии (экспоненциальной) приведен в листинге 15.13 и на рис. 15.17. В предпоследней строке листинга выведены в виде вектора вычисленные коэффициенты а,ь,с, а в последней строке через эти коэффициенты определена искомая функция f (х).
Многие задачи регрессии данных различными двухпараметрическими зависимостями у (х) можно свести к более надежной, с вычислительной точки зрения, линейной регрессии. Делается это с помощью соответствующей замены переменных.
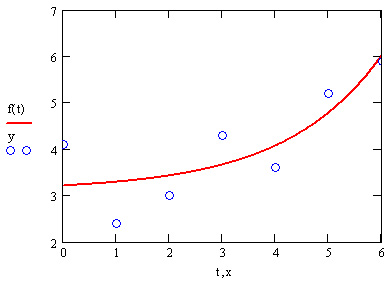
Рис. 15.17. Экспоненциальная регрессия (листинг 15.13)
В Mathcad можно осуществить регрессию в виде линейной комбинации C1f1(x)+C2f2 (х) + ..., где fi(х) — любые функции пользователя, a Ci — подлежащие определению коэффициенты. Кроме того, имеется путь проведения регрессии более общего вида, когда комбинацию функций и искомых коэффициентов задает сам пользователь.
Приведем встроенные функции для регрессии общего вида и примеры их использования (листинги 15.14 и 15.15), надеясь, что читатель при необходимости найдет более подробную информацию об этих специальных возможностях в справочной системе и Mathcad Resources.
- linfit(x,y,F) — вектор параметров линейной комбинации функций пользователя, осуществляющей регрессию данных;
- genfit (x,y,g,G) — вектор параметров, реализующих регрессию данных с помощью функций пользователя общего вида;
- х — вектор действительных данных аргумента, элементы которого расположены в порядке возрастания;
- у — вектор действительных значений того же размера;
- F(X) — пользовательская векторная функция скалярного аргумента;
- g — вектор начальных значений параметров регрессии размерности N;
- G(x,o — векторная функция размерности N+I, составленная из функции пользователя и ее N частных производных по каждому из параметров C.
Листинг 15.14. Регрессия линейной комбинацией функций пользователи
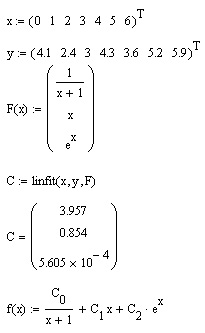
Листинг 15.15. Регрессия общего вида
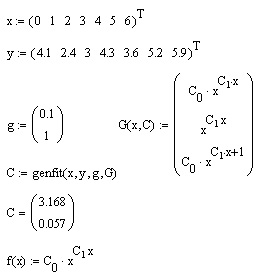
15.3. Сглаживание и фильтрация
При анализе данных часто возникает задача их фильтрации, заключающаяся в устранении одной из составляющих зависимости y(xi). Наиболее часто целью фильтрации является подавление быстрых вариаций y(xi), которые чаще всего обусловлены шумом. В результате из быстроосциллирующей зависимости y(xi) получается другая, сглаженная зависимость, в которой доминирует более низкочастотная составляющая.
Наиболее простыми и эффективными рецептами сглаживания (smoothing) можно считать регрессию различного вида (см. разд. 15.2). Однако регрессия часто уничтожает информативную составляющую данных, оставляя лишь наперед заданную пользователем зависимость.
Часто рассматривают противоположную задачу фильтрации — устранение медленно меняющихся вариаций в целях исследования высокочастотной составляющей. В этом случае говорят о задаче устранения тренда. Иногда интерес представляют смешанные задачи выделения среднемасштабных вариаций путем подавления как более быстрых, так и более медленных вариаций. Одна из возможностей решения связана с применением полосовой фильтрации.
Несколько примеров программной реализации различных вариантов фильтрации приведены в данном разделе.
15.3.1. Встроенные функции для сглаживания
В Mathcad имеется несколько встроенных функций, реализующих различные алгоритмы сглаживания данных.
- medsmooth(y,b) — сглаживание алгоритмом "бегущих медиан";
- ksmooth(x,y,b) — сглаживание на основе функции Гаусса;
- supsmooth(x,y) — локальное сглаживание адаптивным алгоритмом, основанное на анализе ближайших соседей каждой пары данных;
- х — вектор действительных данных аргумента (для supsmooth его элементы должны быть расположены в порядке возрастания);
- у — вектор действительных значений того же размера, что и х;
- b — ширина окна сглаживания.
Все функции имеют в качестве аргумента векторы, составленные из массива данных, и выдают в качестве результата вектор сглаженных данных того же размера. Функция medsmooth предполагает, что данные расположены равномерно.
Подробную информацию об алгоритмах, заложенных в функции сглаживания, Вы найдете в справочной системе Mathcad в статье Smoothing (Сглаживание), находящейся в разделе Statistics (Статистика).
Часто бывает полезным совместить сглаживание с последующей интерполяцией или регрессией. Соответствующий пример приведен в листинге 15.16 для функции supsmooth. Результат работы листинга показан на рис. 15.18 (кружки обозначают исходные данные, крестики — сглаженные, пунктирная кривая — результат сплайн-интерполяции). Сглаживание тех же данных при помощи "бегущих медиан" и функции Гаусса с разным значением ширины окна пропускания показаны на рис. 15.19 и 15.20, соответственно.
Листинг 15.16. Сглаживание с последующей сплайн-интерполяцией

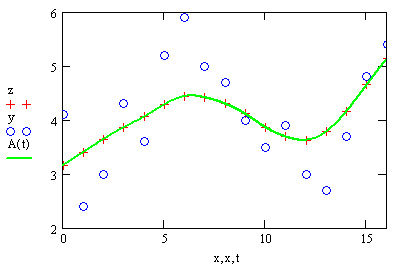
Рис. 15.18. Адаптивное сглаживание (листинг 15.16)
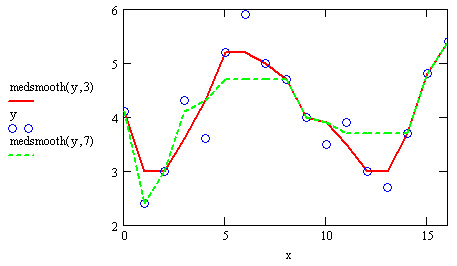
Рис. 15.19. Сглаживание "бегущими медианами"
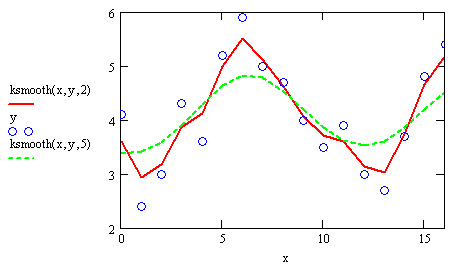
Рис. 15.20. Сглаживание при помощи функции ksmooth
Помимо встроенных в Mathcad, существует несколько популярных алгоритмов сглаживания, на одном из которых хочется остановиться особо. Самый простой и очень эффективный метод — это скользящее усреднение. Его суть состоит в расчете для каждого значения аргумента среднего значения по соседним w данным. Число w называют окном скользящего усреднения; чем оно больше, тем больше данных участвуют в расчете среднего, тем более сглаженная кривая получается. На рис. 15.21 показан результат скользящего усреднения одних и тех же данных (кружки) с разным окном w=3
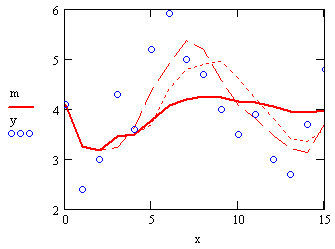
Рис. 15.21. Скользящее усреднение с разными w=3,5,15 (листинг 15.17, коллаж трех графиков)
(пунктир), w=5 (штрихованная кривая) и w=is (сплошная кривая) Видно, что при малых w сглаженные кривые практически повторяют ход изменения данных, а при больших w — отражают лишь закономерность их медленных вариаций
Чтобы реализовать в Mathcad скользящее усреднение, достаточно очень простой программы, приведенной в листинге 15.17. Она использует только значения у, оформленные в виде вектора, неявно предполагая, что они соответствуют значениям аргумента х, расположенным через одинаковые промежутки Вектор х применялся лишь для построения графика результата (рис 15.21)
Листинг 15.17. Сглаживание скользящим усреднением
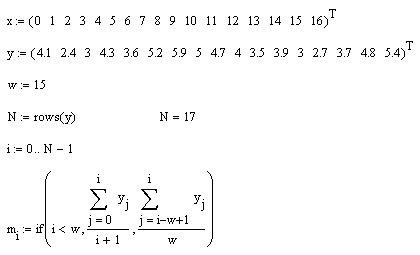
Приведенная программная реализация скользящего усреднения самая простая, но не самая лучшая Возможно Вы обратили внимание, что все кривые скользящего среднего на рис 15.21 слегка "обгоняют" исходные данные Почему так происходит, понятно согласно алгоритму, заложенному в последнюю строку листинга 15.17, скользящее среднее для каждой точки вычисляется путем усреднения значений предыдущих w точек Чтобы результат скользящего усреднения был более адекватным лучше применить центрированный алгоритм расчета по w/2 предыдущим и w/2 последующим значениям Он будет немного сложнее, поскольку придется учитывать недостаток точек не только в начале (как это сделано в программе с помощью функции условия if) но и в конце массива исходных данных.
Еще одна типичная задача возникает, когда интерес исследований заключается не в анализе медленных (или низкочастотных) вариаций сигнала у(х) (для чего применяется сглаживание данных), а в анализе быстрых его изменений Часто бывает, что быстрые (или высокочастотные) вариации накладываются определенным образом на медленные, которые обычно называют трендом. Часто тренд имеет заранее предсказуемый вид, например линейный. Чтобы устранить тренд, можно предложить последовательность действий, реализованную в листинге 15.18.
- Вычислить регрессию f(x), например линейную, исходя из априорной информации о тренде (предпоследняя строка листинга).
- Вычесть из данных у (х) тренд f (x) (последняя строка листинга).
Листинг 15.18. Устранение тренда

На рис. 15.22 показаны исходные данные (кружками), выделенный с помощью регрессии линейный тренд (сплошной прямой линией) и результат устранения тренда (пунктир, соединяющий крестики).
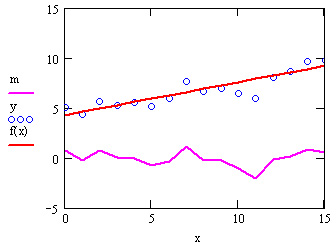
Рис. 15.22. Устранение тренда (листинг 15.18)
В предыдущих разделах была рассмотрена фильтрация быстрых вариаций сигнала (сглаживание) и его медленных вариаций (снятие тренда). Иногда требуется выделить среднемасштабную составляющую сигнала, уменьшив как более быстрые, так и более медленные его компоненты. Одна из возможностей решения этой задачи связана с применением полосовой фильтрации на основе последовательного скользящего усреднения.
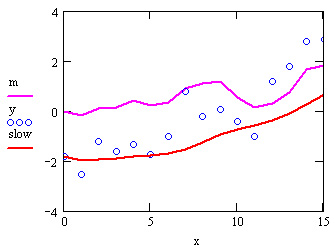
Рис. 15.23. Результат полосовой фильтрации (листинг 15.19)
Алгоритм полосовой фильтрации приведен в листинге 15.19, а результат его применения показан на рис. 15.23 сплошной кривой. Алгоритм реализует такую последовательность операций:
- Приведение массива данных у к нулевому среднему значению путем его вычитания из каждого элемента у (третья и четвертая строки листинга).
- Устранение из сигнала у высокочастотной составляющей, имеющее целью получить сглаженный сигнал middle, например с помощью скользящего усреднения с малым окном w (в листинге 15.19 w=3).
- Выделение из сигнала middle низкочастотной составляющей slow, например, путем скользящего усреднения с большим окном w (в листинге 15.19 w=7) либо с помощью снятия тренда (см. разд. 15.3.3).
- Вычитание из сигнала middle тренда slow (последняя строка листинга), тем самым выделяя среднемасштабную составляющую исходного сигнала у.
Листинг 15.19. Полосовая фильтрация

15.4. Интегральные преобразования
Интегральные преобразования массива сигнала у(х) ставят в соответствие всей совокупности данных у(х) некоторую функцию другой координаты F(V). Рассмотрим встроенные функции для расчета интегральных преобразований, реализованных в Mathcad.
Математический смысл преобразования Фурье состоит в представлении сигнала у(х) в виде бесконечной суммы синусоид вида F(v)sin(vx). Функция F(v) называется преобразованием Фурье или интегралом Фурье, или Фурье-спектром сигнала. Ее аргумент v имеет смысл частоты соответствующей составляющей сигнала. Обратное преобразование Фурье переводит спектр F(V) в исходный сигнал у(х). Согласно определению,
Как видно, преобразование Фурье является существенно комплексной величиной, даже если сигнал действительный.
Преобразование Фурье действительных данных
Преобразование Фурье имеет огромное значение для различных математических приложений, и для него разработан очень эффективный алгоритм, называемый БПФ (быстрым преобразованием Фурье). Этот алгоритм реализован в нескольких встроенных функциях Mathcad, различающихся нормировками.
- fft(y) — вектор прямого преобразования Фурье;
- FFT(Y) — вектор прямого преобразования Фурье в другой нормировке;
- ifft(v) — вектор обратного преобразования Фурье;
- IFFT(V) — вектор обратного преобразования Фурье в другой нормировке;
- у — вектор действительных данных, взятых через равные промежутки значений аргумента;
- v — вектор действительных данных Фурье-спектра, взятых через равные промежутки значений частоты.
Аргумент прямого Фурье-преобразования, т. е. вектор у, должен иметь ровно 2n элементов (n — целое число). Результатом является вектор с 1+2n-1 элементами. И наоборот, аргумент обратного Фурье-преобразования должен иметь 1+2n-1 элементов, а его результатом будет вектор из 2n элементов. Если число данных не совпадает со степенью 2, то необходимо дополнить недостающие элементы нулями.
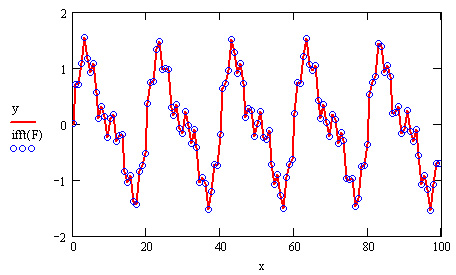
Рис. 15.24. Исходные данные и обратное преобразование Фурье (листинг 15.20)
Пример расчета Фурье-спектра для суммы трех синусоидальных сигналов разной амплитуды (показанных в виде сплошной кривой на рис. 15.24), приведен в листинге 15.20. Расчет проводится по N=128 точкам, причем предполагается, что интервал дискретизации данных ух равен А. В предпоследней строке листинга применяется встроенная функция if ft, а в последней корректно определяются соответствующие значения частот Qx. Обратите внимание, что результаты расчета представляются в виде модуля Фурье-спектра (рис. 15.25), поскольку сам спектр является комплексным. Очень полезно сравнить полученные амплитуды и местоположение пиков спектра с определением синусоид в листинге 15.20.
Листинг 15.20. Быстрое преобразование Фурье
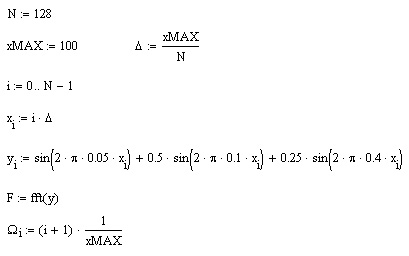
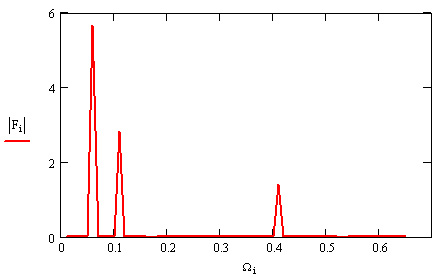
Рис. 15.25. Преобразование Фурье (листинг 15.20)
Результат обратного,преобразования Фурье показан в виде кружков на том же рис. 15.24, что и исходные данные. Видно, что в рассматриваемом случае сигнал у(х) восстановлен с большой точностью, что характерно для плавного изменения сигнала.
Преобразование Фурье комплексных данных
Алгоритм быстрого преобразования Фурье для комплексных данных встроен в соответствующие функции, в имя которых входит литера "с".
- cfft(y) — вектор прямого комплексного преобразования Фурье;
- CFFT(y) — вектор прямого комплексного преобразования Фурье в другой нормировке;
- icfft(y) —вектор обратного комплексного преобразования Фурье;
- ICFFT(V) — вектор обратного комплексного преобразования Фурье в другой нормировке;
- у — вектор данных, взятых через равные промежутки значений аргумента;
- v — вектор данных Фурье-спектра, взятых через равные промежутки значений частоты.
Функции действительного преобразования Фурье используют тот факт, что в случае действительных данных спектр получается симметричным относительно нуля, и выводят только его половину (см. выше разд. "Преобразование Фурье действительных данных" этой главы). Поэтому, в частности, по 128 действительным данным получалось всего 65 точек спектра Фурье. Если к тем же данным применить функцию комплексного преобразования Фурье (рис. 15.26), то получится вектор из 128 элементов. Сравнивая рис. 15.25 и 15.26, можно уяснить соответствие между результатами действительного и комплексного Фурье-преобразования.
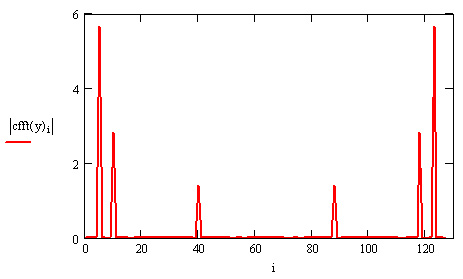
Рис. 15.26. Комплексное преобразование Фурье (продолжение листинга 15.20)
Двумерное преобразование Фурье
В Mathcad имеется возможность применять встроенные функции комплексного преобразования Фурье не только к одномерным, но и к двумерным массивам, т. е. матрицам. Соответствующий пример приведен в листинге 15.21 и на рис. 15.27 в виде графика линий уровня исходных данных и рассчитанного Фурье-спектра.
Листинг 15.21. Двумерное преобразование Фурье

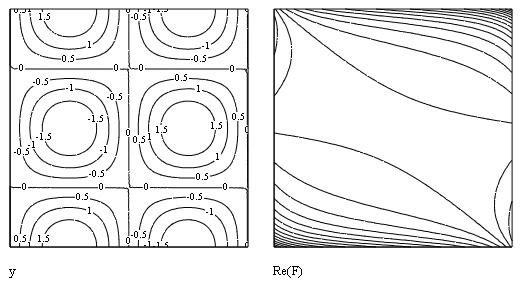
Рис. 15.27. Данные (слева) и их Фурье-спектр (справа) (листинг 15.21)
15.4.2. Вейвлетное преобразование
В последнее время возрос интерес к другим интегральным преобразованиям, в частности вейвлетному (или дискретному волновому) преобразованию. Оно применяется, главным образом, для анализа нестационарных сигналов и для многих задач подобного рода оказывается более эффективным, чем преобразование Фурье. Основным отличием вейвлетного преобразования является разложение данных не по синусоидам (как для преобразования Фурье), а по другим функциям, называемым вейвлетобразующими. Вейвле-тобразующие функции, в противоположность бесконечно осциллирующим синусоидам, локализованы в некоторой ограниченной области своего аргумента, а вдали от нее равны нулю или ничтожно малы. Пример такой функции, называемой "мексиканской шляпой", показан на рис. 15.28.
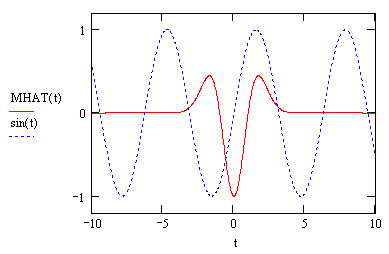
Рис. 15.28. Сравнение синусоиды и вейвлетобразующей функции
Из-за своего математического смысла вейвлет-спектр имеет не один аргумент, а два. Помимо частоты, вторым аргументом ь является место локализации вейвлетобразующей функции. Поэтому b имеет ту же размерность, что и х.
Встроенная функция вейвлет-преобразования
Mathcad имеет одну встроенную функцию для расчета вейвлет-преобразования на основе вейвлетобразующей функции Даубечи.
- wave (у) — вектор прямого вейвлет-преобразования;
- iwave(v) —вектор обратного вейвлет-преобразования;
- у — вектор данных, взятых через равные промежутки значений аргумента;
- v — вектор данных вейвлет-спектра.
Аргумент функции вейвлет-преобразования, т. е. вектор у, должен так же, как и в преобразовании Фурье, иметь ровно 2n элементов (n — целое число). Результатом функции wave является вектор, скомпонованный из нескольких коэффициентов с двухпараметрического вейвлет-спектра. Использование функции wave объясняется на примере анализа суммы двух синусоид в листинге 15.22, а три семейства коэффициентов вычисленного вейвлет-спектра показаны на рис. 15.29.
Листинг 15.22. Поиск вейлет-спектра Даубечи

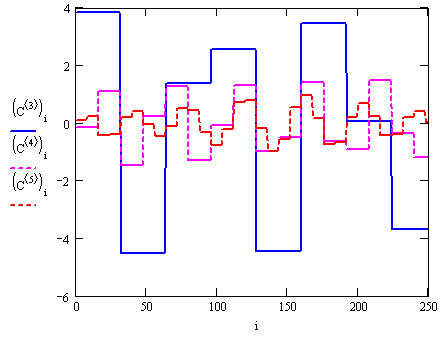
Рис. 15.29. Вейвлет-спектр на основе функции Даубечи (листинг 15.22)
Программирование других вейвлет-преобразований
Помимо встроенной функции вейвлет-спектра Даубечи и возможностей пакета расширения Mathcad 11, возможно непосредственное программирование алгоритмов пользователя для расчета вейвлет-спектров. Оно сводится к аккуратному расчету соответствующих семейств интегралов. Один из примеров такой программы приведен в листинге 15.23, а ее результат на рис. 15.30. Анализу подвергается та же функция, составленная из суммы двух синусов, а график двухпараметрического спектра с(а,b) выведен в виде привычных для вейвлет-анализа линий уровня на плоскости (а,b).
Листинг 15.23. Поиск вейвлет-спектра на основе "мексиканской шляпы"
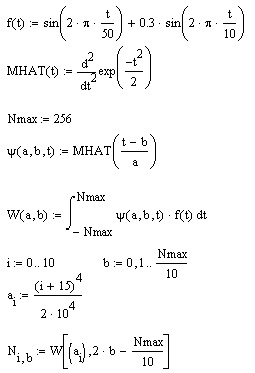
Программа листинга очень проста, но исключительно далека от хорошей в смысле быстродействия. Каждый интеграл вычисляется независимо, без использования методов ускорения, типа применяемых в алгоритме БПФ.
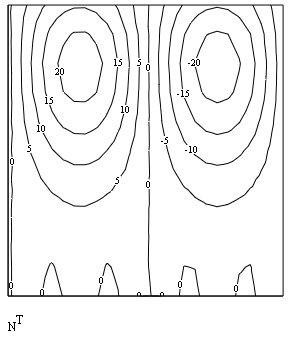
Рис. 15.30. Вейвлет-спектр на основе "мексиканской шляпы" (листинг 15.23)