Специальные функции

• 10.1. Функции Бесселя (Bessel)
  • 10.1.1. Обычные функции Бесселя
  • 10.1.2. Модифицированные функции Бесселя
  • 10.1.3. Функции Эйри
  • 10.1.4. Функции Бесселя-Кельвина
  • 10.1.5. Сферические функции Бесселя
• 10.2. Функции работы с комплексными числами (Complex Numbers)
• 10.3. Логарифмы и экспонента (Log and Exponential)
• 10.4. Тригонометрические функции (Trigonometric)
• 10.5. Гиперболические функции (Hyperbolic)
• 10.6. Другие спецфункции (Special)
• 10.7. Строковые функции (String)
• 10.8. Функции сокращения и округления (Truncation and Round-Off)
• 10.9. Кусочно-непрерывные функции (Piecewise Continuous)
• 10.10. Функции преобразования координат (Vector and Matrix)
• 10.11. Финансовые функции (Finance)

Данная глава посвящена вычислению различных математических функций, встроенных в Mathcad. Причем описываются как специальные функции (Бесселя, Эйри и т. п.), так и элементарные функции (синус, экспонента, гиперболические функции), а также функции, специфичные для тех или иных областей (финансовые функции). Кроме того, упоминаются очень простые, с точки зрения программной реализации, но часто очень полезные функции типа ступеньки, дельта - функции и т. д.

Несмотря на то, что большинство функций, о которых пойдет речь в этой главе, рассчитываются без привлечения специальных численных методов, мы совместили рассказ о них в одной главе, чтобы читателю было удобнее найти описание нужной функции. Перечень специальных функций разбит на разделы по их математическому смыслу и (или) области применения.

Вставлять в документ не очень знакомую спецфункцию легче всего, пользуясь диалоговым окном Insert Function (Вставить функцию), которое вызывается нажатием кнопки с надписью f(x) на стандартной панели инструментов (см. разд. "Знакомство с Mathcad" гл. 1). В этом диалоге функции разбиты на несколько групп, поэтому несложно выбрать из них нужную. При выделении какой-либо группы в левом списке упомянутого диалога справа обнаруживается список функций, принадлежащих этой группе. Названия групп функций, появляющихся в левом списке диалогового окна Insert Function, приведены в скобках после названия каждого раздела этой главы.

10.1. Функции Бесселя (Bessel)

Функции Бесселя, по определению, являются решениями различных краевых задач для некоторых обыкновенных дифференциальных уравнений (ОДУ).

10.1.1. Обычные функции Бесселя

Функции Бесселя первого и второго рода обычно возникают как решения волнового уравнения с цилиндрическими граничными условиями.

Конкретный вид соответствующих дифференциальных уравнений можно без труда отыскать в справочниках по спецфункциям или в справочной системе Mathcad.

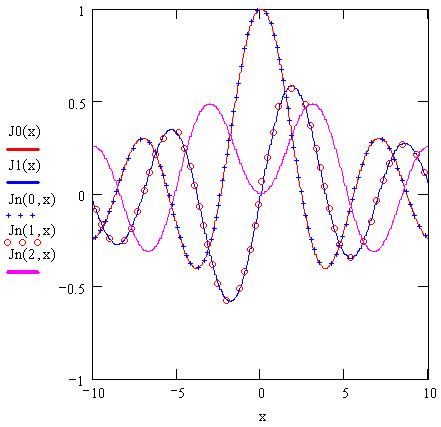
Рис. 10.1. Функции Бесселя первого рода

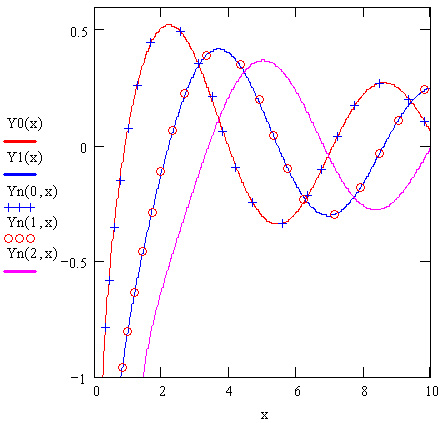
Рис. 10.2. Функции Бесселя второго рода

• J0(z) — функция Бесселя первого рода нулевого порядка;
• J1(z) — функция Бесселя первого рода первого порядка;
• Jn(m, z) — функция Бесселя т-го порядка;
• Y0(z) — функция Бесселя второго рода нулевого порядка, х>0;
• Y1(z) — функция Бесселя второго рода первого порядка, х>0;
• Yn(m, z) — функция Бесселя второго рода m-го порядка, х>0;
• z — действительный или комплексный безразмерный скаляр;
• m — порядок, целое число 0<m<100.

Внешний вид нескольких первых функций Бесселя первого и второго рода показан на рис. 10.1 и 10.2, соответственно.

10.1.2. Модифицированные функции Бесселя

Перечислим их:

• I0(z) — модифицированная функция Бесселя первого рода нулевого порядка;
• I1(z) — модифицированная функция Бесселя первого рода первого порядка;
• In(m,z) — модифицированная функция Бесселя первого рода m-го порядка;
• K0(z) — модифицированная функция Бесселя второго рода нулевого порядка, х>0;
• K1(z) — модифицированная функция Бесселя второго рода первого порядка, х>0;
• Kn(m,z) — модифицированная функция Бесселя второго рода m-го порядка, х>0;
• z — действительный или комплексный безразмерный скаляр;
• m — порядок, целое число 0<m<100.

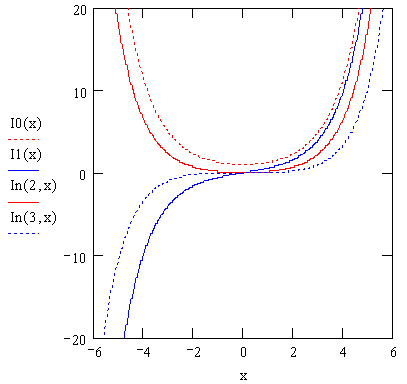
Рис. 10.3. Модифицированные функции Бесселя первого рода

Примеры нескольких первых модифицированных функций Бесселя показаны на рис. 10.3 и 10.4.

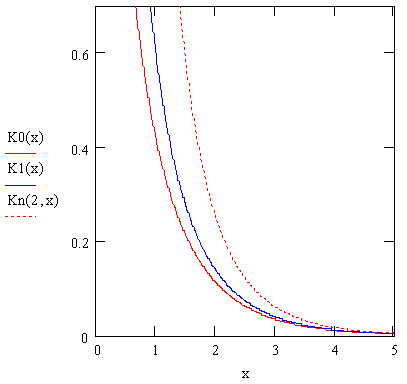
Рис. 10.4. Модифицированные функции Бесселя второго рода

10.1.3. Функции Эйри

Функции Эйри являются независимыми решениями ОДУ y' '=zy. Их вид показан на рис. 10.5. Итак:

• Ai (z) — функция Эйри первого рода;
• Bi (z) — функция Эйри второго рода;
• z — действительный или комплексный безразмерный скаляр, х<103.892.

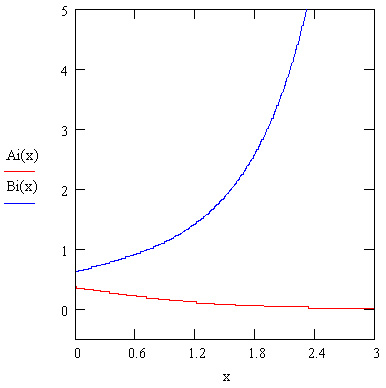
Рис. 10.5. Функции Эйри

10.1.4. Функции Бесселя-Кельвина

Комплексная комбинация функций Бесселя-Кельвина вида ber(n,x) + i bei(n,x) является решением соответствующего ОДУ, зависящего от параметра n. Вид графиков функции bei для n=i и 2 показан на рис. 10.6.

• bei (n,x) — мнимая часть функции Бесселя-Кельвина порядка n;
• ber(n,x) — действительная часть функции Бесселя-Кельвина порядка n;
• n — порядок (безразмерное неотрицательное целое число);
• х — действительный безразмерный скаляр.

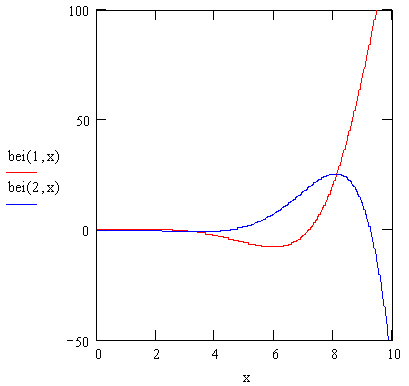
Рис. 10.6. Функции Бесселя-Кельвина

10.1.5. Сферические функции Бесселя

График сферических функций Бесселя первого порядка показан на рис. 10.7.

• js(n, z) — сферическая функция Бесселя первого рода порядка n, х>0;
• ys (n, z) — сферическая функция Бесселя второго рода порядка n, х>0;
• n — порядок (целое число), n>200;
• z — действительный или комплексный безразмерный скаляр, х>0.

10.2. Функции работы с комплексными числами (Complex Numbers)

В Mathcad имеется несколько функций, облегчающих работу с комплексными числами.

• Re(z) — действительная часть комплексного числа z;
• im(z) — мнимая часть комплексного числа z;

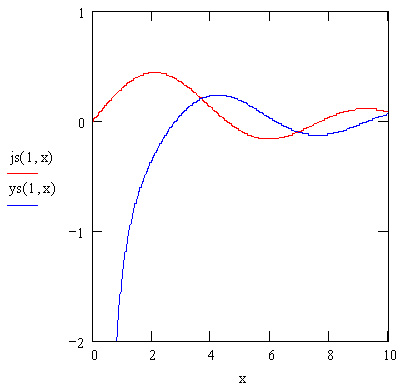
Рис. 10.7. Сферические функции Бесселя первого порядка

• arg(z) — аргумент комплексного числа z, --pi<arg(z)<pi;
• csgn(z) — функция комплексного знака числа (возвращает либо 0, если z=0; либо 1, если Re(z)>0, или если Re(z)=o и im(z)>0; либо -1 — в остальных случаях);
• signum(z) — возвращает 1, если z=0, и z/|z| — в остальных случаях;
• z — действительное, мнимое или комплексное число.

Комплексное число можно ввести как обычно, в виде суммы действительной и мнимой частей, либо как результат любого комплексного выражения. Несколько примеров действия функций работы с комплексными числами приведены в листингах 10.1—10.3.

Листинг 10.1. Базовые функции работы с комплексными числами

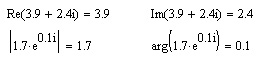
Листинг 10.2. Пример действия функции csgn

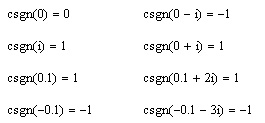
Листинг 10.3. Пример действия функции signum

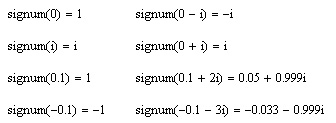
10.3. Логарифмы и экспонента (Log and Exponential)

Перечислим без комментариев хорошо известные логарифмические функции (рис. 10.8) и экспоненциальную функцию:

• exp(z) — значение е (основание натурального логарифма) в степени z;
• ln (z) — натуральный логарифм;
• log(z) — десятичный логарифм;
• log(z,b) — логарифм z по основанию b.
• lnGamma(z) — логарифм гамма-функции Эйлера (см. разд 10.6);

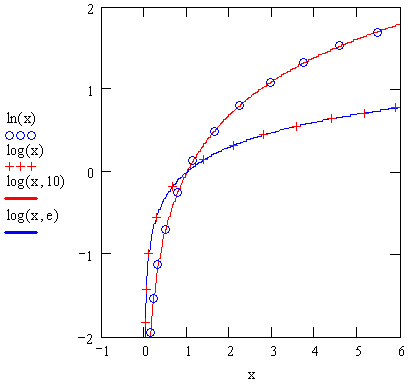
Рис. 10.8. Логарифмические функции

10.4. Тригонометрические функции (Trigonometric)

• acos(z) —арккосинус;
• acot(z) — котангенс;
• acsc(z) — арккосеканс (листинг 10.4);
• angle(x,y) — угол между точкой (х,у) и осью ох;
• asec(z) — арксеканс;
• asin(z) — арксинус (листинг 10.4);
• atan (z) — арктангенс;
• atan2(x,y) — угол, отсчитываемый от оси ОХ до точки (х,у) (листинг 10.5);
• cos(z) —косинус;
• cot(z) — котангенс;
• csc(z) — косеканс (листинг 10.4);
• sec(z) —секанс;
• sin(z) — синус (листинг 10.4);
• tan(z) — тангенс;
• z — безразмерный скаляр.

Аргумент тригонометрических функций и результат обратных тригонометрических функций выражаются в радианах. Чтобы использовать значение угла в градусах, его необходимо перевести в радианы (листинг 10.6). Аргумент тригонометрических функций может быть комплексным.

Листинг 10.4. Примеры тригонометрических функций

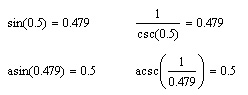
Листинг 10.5. Примеры расчета угла между прямой и осью OX

Листинг 10.6. Расчет тригонометрических функций в градусах

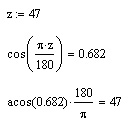
10.5. Гиперболические функции (Hyperbolic)

Гиперболические функции, согласно определению, выражаются через различные комбинации ez и е~г (пример приведен в листинге 10.7). Аргумент гиперболических функций также может быть комплексным. Графики трех основных гиперболических функций показаны на рис. 10.9.

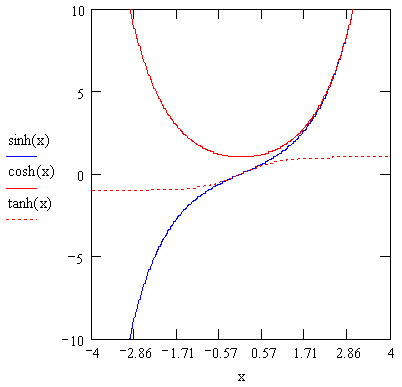
Рис. 10.9. Основные гиперболические функции

• acosh(z) — гиперболический арккосинус;
• acoth(z) — гиперболический котангенс;
• asinh(z) — гиперболический арксинус;
• acsch(z) — гиперболический арккосеканс;
• atanh(z) — обратный гиперболический тангенс;
• asech(z) — обратный гиперболический секанс;
• cosh(z) —гиперболический косинус;
• coth(z) — гиперболический котангенс;
• sinh(z) — гиперболический синус;
• csch(z) — гиперболический косеканс;
• tanh(z) — гиперболический тангенс;
• sech(z) —гиперболический секанс;
• z — безразмерный скаляр.

Листинг 10.7. Пример гиперболических функций

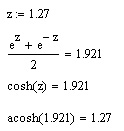
10.6. Другие спецфункции (Special)

Приведем перечень остальных спецфункций, которые рассчитываются Mathcad встроенным образом. Действие некоторых функций иллюстрируется листингом 10.8, а некоторые полиномы — графиками на рис. 10.11—10.13.

• erf (z) — функция ошибок (см. разд. "Нормальное (Гауссово) распределение" гл. 14)
• erfc(z)=1-erf(z);
• z — скаляр.
• fhyper(а,b,с,х) —Гауссова гипергеометрическая функция;
• mhyper(a,b,x) — конфлюэнтная гипергеометрическая функция;
• а, b, с — параметры;
• х — действительный скаляр, -1<х<1.
• Gamma (z) — гамма-функция Эйлера;
• z — скаляр, |z|<1.
• Gamma (а, х) — неполная гамма-функция порядка а;
• х — действительный положительный скаляр.

Гамма-функция в документе Mathcad отображается греческой буквой Г (листинг 10.8).

• нег(n,х) — полином Эрмита порядка n с аргументом х (рис. 10.10);
• n — порядок (неотрицательное целое число);
• х — скаляр.

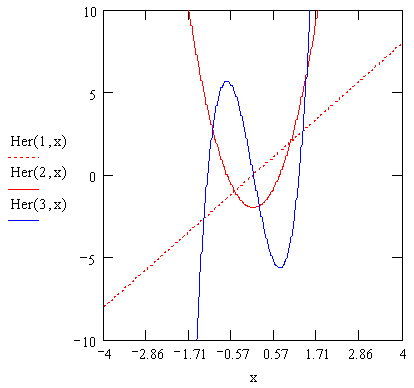
Рис. 10.10. Полиномы Эрмита

• ibeta(a,x,y) — неполная бета-функция для х и у с параметром а;
• а — действительный скаляр, 0<a<i;
• х,у — действительные скаляры, х>0, у>0.
• Jac (n, а, b, х) — полином Якоби степени n в точке х с параметрами а и b;
• Lag(n,x) — полином Лагерра степени n в точке х (рис. 10.11);

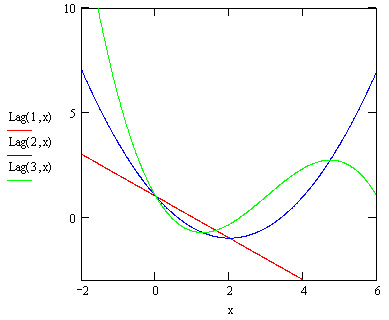
Рис. 10.11. Полиномы Лаггера

• Leg(n,x) — полином Лежандра степени п в точке х (рис. 10.12);
• n — порядок (неотрицательное целое число);
• х - действительный скаляр;
• а,b — действительные скаляры, а>-1, b>-1.
• Tcheb(n,x) — полином Чебышева первого рода степени n в точке х (рис. 10.13);
• Ucheb(n,x) — полином Чебышева второго рода степени n в точке х (рис. 10.13);
• n — порядок (неотрицательное целое число);
• х — действительный скаляр.

Листинг 10.8. Примеры вычисления некоторых спецфункций

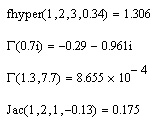
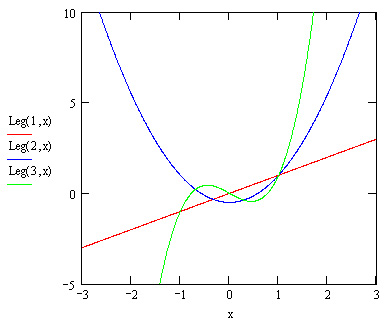
Рис. 10.12. Полиномы Лежандра

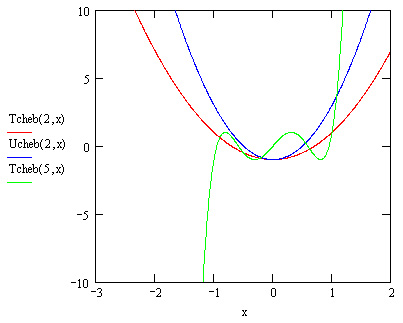
Рис. 10.13. Полиномы Чебышева

10.7. Строковые функции (String)

Приведем перечень функций, благодаря которым пользователь может оперировать со строковыми переменными, подобно операциям с числами:

• concat(s1,s2,...) — строковая переменная, полученная объединением строковых переменных или констант s1, S2,... (листинг 10.9);
• error (S) — возвращает строку s как сообщение об ошибке (рис. 10.14);
• lsString(x) — возвращает 1, если х строковая переменная, и 0 — в остальных случаях (листинг 10.10);
• num2str(z) — возвращает строку, чьи знаки соответствуют десятичному значению числа z (листинг 10.10);

Функция num2str(z) используется, когда проще манипулировать с числом как со строкой, нежели как с математической переменной.

• search(s,Subs,m) — стартовая позиция подстроки subs в строке s при поиске, начиная с позиции m, при неуспешном поиске возвращает -1 (листинг 10.9);
• str2num(s) — преобразование строкового представления числа s (в любой форме) в число (листинг 10.10);
• str2vec(s) — преобразование в вектор ASCII-кодов строки s (листинг 10.10);
• strlen(s) — количество знаков в строке s (листинги 10.9, 10.10);
• substr <s,m,n) — подстрока, полученная из строки s выделением n знаков, начиная с позиции m в строке s (листинг 10.9);
• vec2str(v) — строковое представление элементов вектора v ASCII-кодов;
• s — строка;
• v — вектор ASCII-кодов (целых чисел, 0<v<255).

Листинг 10.9. Примеры использования строковых функций

Листинг 10.10. Функции взаимных преобразований чисел и строк

Рис. 10.14. Использование функции создания сообщения об ошибке

10.8. Функции сокращения и округления (Truncation and Round-Off)

• ceil(z) — наименьшее целое, не меньшее z (листинг 10 11);
• floor (z) — наибольшее целое число, меньшее или равное z (листинг 10 11);
• round(z,n) — при n>0 возвращает округленное значение z с точностью до n знаков после десятичной точки, при n<0 — округленное значение z с n цифрами слева от десятичной точки, при n=0 — округленное до ближайшего целого значение z (листинг 10 12);
• trunc(z) — целая часть числа (листинг 10 11);
• z — действительный или комплексный скаляр

Начиная с версии Mathcad 11 функции округления и сокращения чисел поддерживают также и комплексные аргументы (последние строки листингов 10.11 и 10.12)

Листинг 10.11. Функции сокращения и округления

Листинг 10.12. Округление чисел

При округлении не забывайте о принципах представления чисел в Mathcad. Чтобы отобразить нужное количество знаков после десятичной точки, воспользуйтесь диалогом Result Format (Формат результата) (см. гл. 4).

10.9. Кусочно-непрерывные функции (Piecewise Continuous)

• heaviside step(x) — функция Хевисайда, возвращает 1, если х>0, и 0 — в остальных случаях (рис. 10.15);
• х — действительный скаляр.
• if (cond,x,y) — возвращает х, если логическое условие cond верно (не ноль), и у в остальных случаях (листинг 10.13);
• Kronecker delta (х, у) — дельта-символ Кронекера: возвращает 1, если х=у, и 0 в остальных случаях (рис. 10.15);
• sign(x) — возвращает 0, если х=0, 1, если х>0, и -1 — в остальных случаях (листинг 10.13);
• х — действительное число.

В документах символ Кронекера обозначается греческой буквлэи б, а функция Хевисайда — буквой Ф.

Листинг 10.13. Функции уловия и знака

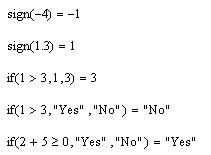
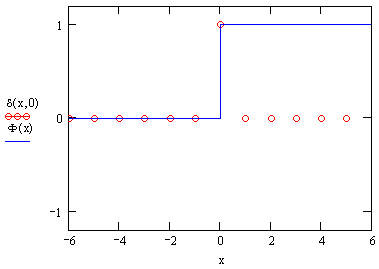
Рис. 10.15. Функции Кронекера и Хевисайда

10.10. Функции преобразования координат (Vector and Matrix)

В Mathcad 2001 появилось семейство новых функций, позволяющих перейти от одних координат к другим, как на плоскости, так и в пространстве:

• xy2pol (х,у) — преобразование прямоугольных координат в полярные;
• роl2ху(r,0) —преобразование полярных координат в прямоугольные;
• angle (х, у) — угол между точкой (х,у) и осью ох (см. разд. 10.4);
• atan2(x,y) — угол, отсчитываемый от оси ох до точки (х,у) (см. разд. 10.4);
• xyz2cyl(x,y,z) — преобразование прямоугольных координат в цилиндрические;
• cyl2xyz (r,0,z) — преобразование цилиндрических координат в прямоугольные;
• xyz2sph(x,y,z) — преобразование прямоугольных координат в сферические;
• sph2xyz(r,0,ф) — преобразование сферических координат в прямоугольные;
• х,у — прямоугольные координаты на плоскости;
• х,у,z — прямоугольные координаты в пространстве;
• r,0 — полярные координаты на плоскости;
• r,0,z — цилиндрические координаты;
• r,0,ф — сферические координаты.

Несколько примеров преобразования координат приведены в листингах 10.14 и 10.15. Обратите внимание на возможность ввода аргументов этих функций как в виде списка, так и в виде вектора.

Листинг 10.14. Функции преобразования координат на плоскости

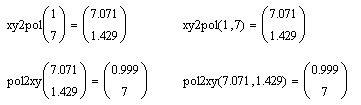
Листинг 10.15. Функции преобразования координат в пространстве

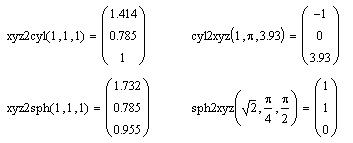
10.11. Финансовые функции (Finance)

Начиная с версии 2000, в Mathcad появились функции, облегчающие финансовый анализ. Приведем список этих функций, не вдаваясь в пояснения и надеясь на то, что заинтересованный читатель найдет подробное описание и практические примеры их применения в справочной системе Mathcad.

• cnper (rate,pv, fv) — отвечает числу составных периодов, необходимых для получения будущего значения вклада при заданных текущем значении вклада и проценте начислений;
• rate — фиксированный процент по вкладу; должен быть действительным скаляром, rate>-i;
• pv — текущее значение вклада, pv>0;
• fv — будущее значение вклада, fv>0.
• crate (nper,pv, fv) — отвечает фиксированному проценту начислений по вкладу на период, необходимый для прироста от текущего значения вклада до будущего значения при заданном числе составных периодов;
• nper — число составных периодов; должно быть целым числом, nper>1;
• pv — текущее значение вклада, pv>0;
• fv — будущее значение вклада, fv>0.
• cumint (rate, nper,pv, start, end, [type] ) — отвечает совокупному проценту по заему между начальным и конечным периодами при фиксированном проценте, общем числе составных периодов и текущем значении заема;
• cumprn (rate, nper,pv, start, end, [type]) — отвечает совокупной сумме по заему между начальным и конечным периодами при фиксированном проценте, общем числе составных периодов и текущем значении заема;
• rate — фиксированный процент по вкладу; должен быть действительным скаляром, rate>0;
• nper — общее число составных периодов; должно быть положительным целым числом;
• pv — текущее значение заема, pv>0;
• start — начальный период накопления; должен быть положительным целым числом;
• end — конечный период накопления; должен быть положительным целым числом; starts end;
• type=0 для платежа, сделанного в конце периода, или 1 для платежа, сделанного в начале периода.
• eff (rate,nper) — отвечает эффективной ежегодной процентной ставке при данной номинальной ежегодной процентной ставке и числе составных периодов в год;
• rate — номинальная процентная ставка; должна быть действительным скаляром;
• nper — общее число составных периодов в год, nper >0.
• fv(rate,nper,pmt, [ [pv], [type] ]) — соответствует будущему значению вклада или заема через особое число составных периодов, установленных периодически, при постоянных платежах и фиксированной процентной ставке;
• rate — фиксированная процентная ставка за период; должна быть действительным скаляром, rate>0;
• nper — общее число составных периодов в год, nper >0;
• pv — текущее значение заема;
• type=0 для платежа, сделанного в конце периода, или 1 для платежа, сделанного в начале периода.
• fvadj (pnn,v) — соответствует будущему значению ежегодной общей суммы капитала, на который начисляются проценты, при применении серии составных процентных ставок;
• рrin — ежегодная общая сумма;
• v — вектор процентных ставок, каждая из которых применяется с той же самой основной суммой и процентами с нее за период времени.
• fvc (rate, v) — соответствует будущему значению серии денежных потоков, происходящих с регулярными интервалами, и приносящими специальную процентную ставку;
• rate — фиксированная процентная ставка за период; должна быть действительным скаляром;
• v — вектор регулярных денежных потоков.
• ipmt (rate, per, nper,pv, [ [fv] , type] ])— соответствует Процентному платежу по вкладу или заему за данный период, основанному на периодичности, постоянных платежах через данное число составных периодов, использующих фиксированную процентную ставку и особое текущее значение;
• rate — фиксированная процентная ставка за период, rate>0;
• per — период, за который Вы хотите найти ставку; должен быть положительным целым числом;
• nрег — общее число составных периодов, per< nper;
• pv - текущее значение;
• fv — будущее значение;
• type=0 для платежа, сделанного в конце периода, или i для для платежа, сделанного в начале периода.
• irr(v, [guess]) — отвечает внутренней ставке возврата для серии денежных потоков, происходящих с регулярными интервалами;
• v — вектор денежных потоков, определяемых за регулярные интервалы, должен состоять по крайней мере из одного положительного и отрицательного числа;
• guess — численное значение, которым Вы предполагаете аппроксимировать ответ, если им пренебрегается, то guess=0.1(10%).
• mirr (v, fm_rate, rem_rate) — соответствует модифицированной процентной ставке возврата для серии денежных потоков с регулярными интервалами при условии, что ставка финансирования подлежит оплате в соответствии с суммой заимствования, а ставка реинвестирования приносит доход с суммы, которую Вы повторно инвестируете;
• v — вектор денежных потоков, определяемых за регулярные интервалы; он должен состоять по крайней мере из одного положительного и отрицательного числа;
• fin_rate — финансовая ставка платежа по заимствованным денежным потокам;
• rem_rate — ставка реинвестирования.
• nom(rate,nper) — соответствует номинальной процентной ставке, включающей эффективную ежегодную процентную ставку и число составных периодов за год;
• rate — эффективная ежегодная процентная ставка; должна быть действительным скаляром, rate>-1;
• nper — общее число составных периодов за год, nреr>0.
• npv(rate,v) — вычисляет чистое текущее значение вклада, включающее скидки и регулярные денежные потоки;
• rate — фиксированная процентная ставка, с которой вклад зарабатывает процент за период; должна быть действительным скаляром;
• v — вектор регулярных денежных потоков.
• nper (rate,pmt,pv, [ [fv], [type] ]) — отвечает числу периодов для вклада или заема, основанных на периодичности, постоянных платежах, использующих фиксированную процентную ставку и особое текущее значение;
• pmt (rate,nper,pv, [ [fv], [type] ]) — соответствует платежу по вкладу или заему, основанному на периодичности, постоянных платежах через данное число составных периодов, использующих фиксированную процентную ставку и особое текущее значение;
• ppmt (rate,per,nper,pv, [ [fv], [type] ]) — соответствует платежу по общей сумме вклада или заема, основанному на периодичности, постоянных платежах через данное число составных периодов, использующих фиксированную процентную ставку и особое будущее значение;
• pv(rate,nper,pmt, [ [fv], [type] ]) — соответствует текущему значению вклада или заема, основанному на периодичности, постоянных платежах через данное число составных периодов, использующих фиксированную процентную ставку и особый взнос;
• rate(nper,pmt,pv, [ [fv] , [type] , [guess] ] ) — соответствует Процентной ставке на период вклада или заема при особом числе периодических составных периодов, постоянных платежах и особом текущем значении;
• rate — фиксированная процентная ставка;
• per — период;
• nper — общее число составных периодов за год; должно быть положительным целым числом;
• pmt — платеж, делаемый каждый период;
• pv — текущее значение вклада;
• fv — будущее значение вклада;
• type=0 для платежа, сделанного в конце периода, или i для платежа, сделанного в начале периода;
• guess — численное значение, которым Вы предполагаете аппроксимировать ответ; если им пренебрегается, то guess=0.01(10%).